图解错位排列
1 对夫妻的比武
如果只有 1 对夫妻,比如张无忌和赵敏,显然他们不能比武,所以比武的方法数为 0:
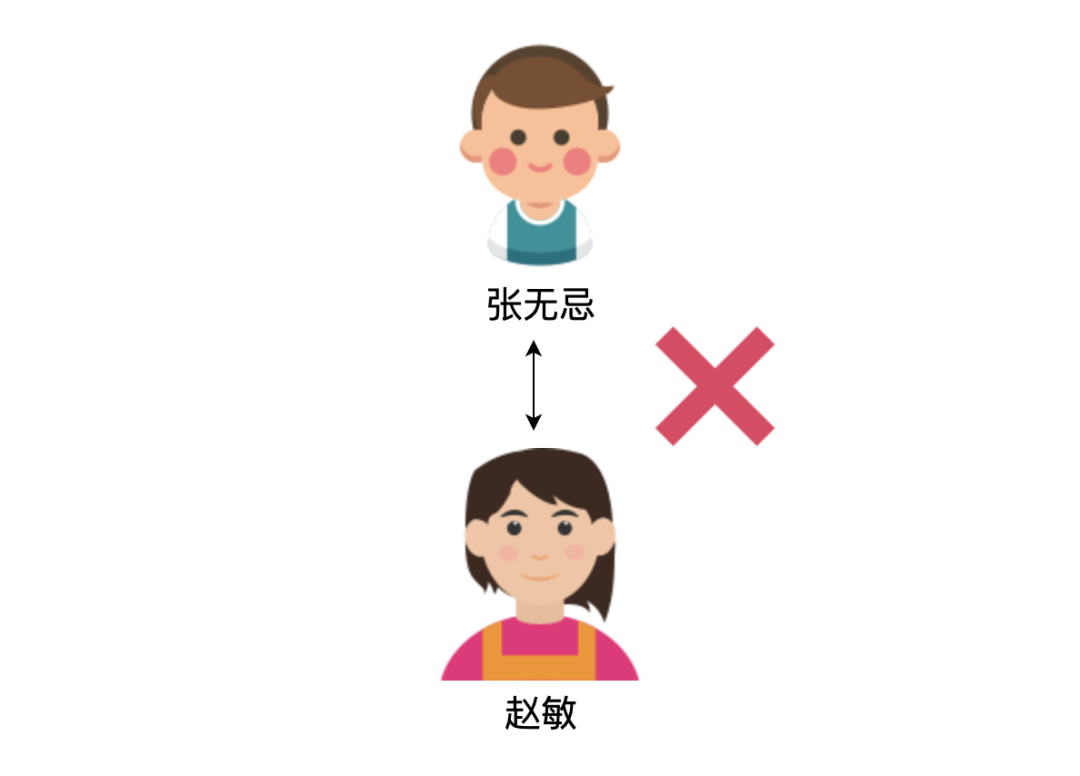
2 对夫妻的比武
如果有 2 对夫妻,很显然,他们的比武安排的方法数是 1,只有唯一的办法,如下:
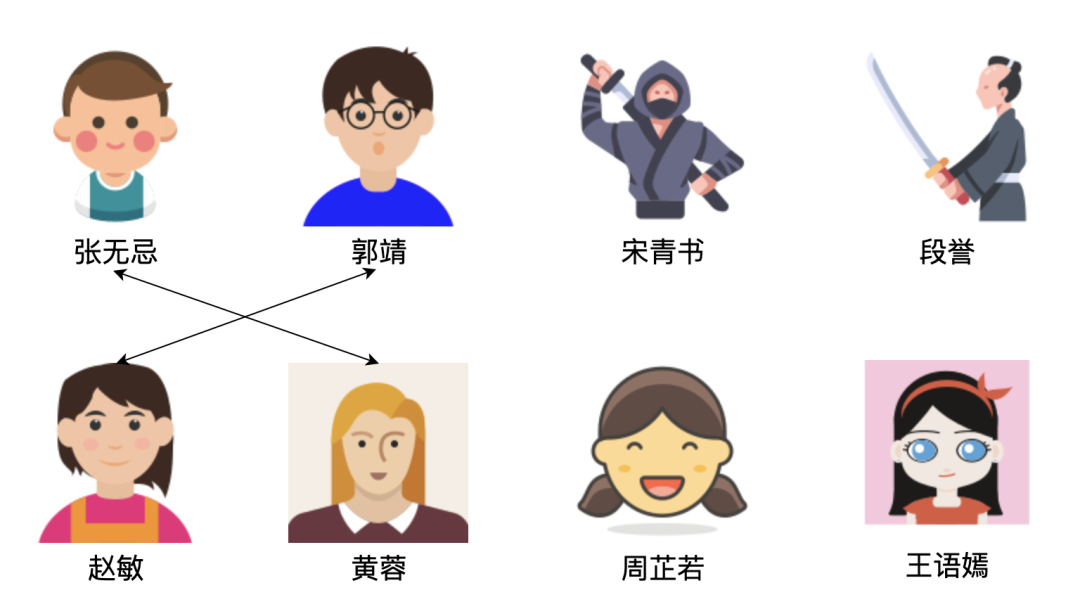
3 对夫妻的比武
如果有 3 对夫妻,可以按照如下图所示的 2 种安排方法进行比武,显然,方法数为 2:

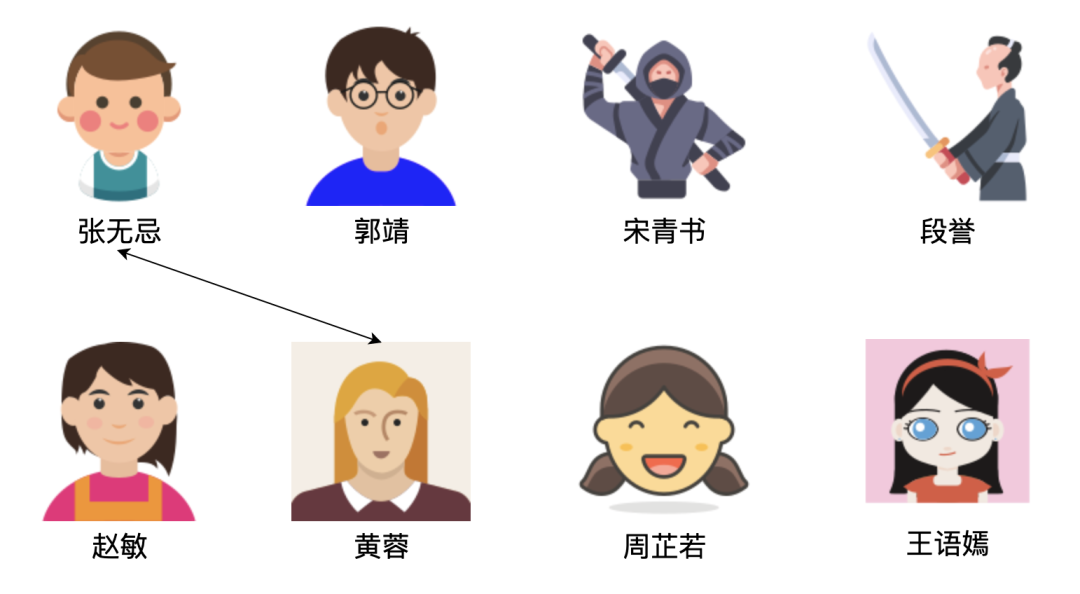
n 对夫妻的比武
接下来,我们看更一般的情况,假设有 n 对夫妻,对应的错位比武方法数为 F(n), 显然有:
| n 的值
| F(n) 的值
|
| n = 1
| 0
|
| n = 2
| 1
|
| n = 3
| 2
|
| n > 3
| ?
|
假设有 n 对夫妻,我们来一起分析下。对于张无忌而言,假设他选择黄蓉,此时,郭靖要么选择赵敏,要么不选择赵敏。我们先考虑郭靖选择赵敏的情况,如下:

可以看到,前面的 2 对夫妻配对好了,后面还有 n-2 对夫妻,他们只要完成错位比武就行。显然,问题的规模缩小了。剩下的 n-2 对夫妻的错位比武的方法数为 F(n-2).
接着看另外一种情况,假设张无忌选择黄蓉后,郭靖不选择赵敏,那么情况如下:

为了更好地理解这种情况,我来调整一下位置,如下:

现在的问题变成了:郭靖不能选择赵敏,宋青书不能选择周芷若,段誉不能选择王语嫣,这不就是规模为 n-1 的错位比武问题吗?是的,方法数为 F(n-1).
综上所述:
- 当张无忌选择黄蓉,郭靖选择赵敏时,整体的错位比武方法数为 F(n-2)
- 当张无忌选择黄蓉,而郭靖不选择赵敏时,整体的错位比武方法数为 F(n-1)
也就是说,当张无忌选择黄蓉时,整体的错位比武方法数为:
F(n-2) + F(n-1)
显然,张无忌除了选择黄蓉外,还可以选择周芷若或者王语嫣,总之,张无忌可选的方法数为 n-1, 所以,整体的错位比武方法数 F(n) 为:
(n-1)*(F(n-2) + F(n-1))
故有:
| n 的值 | F(n) 的值 |
|---|---|
| n = 1 | 0 |
| n = 3 | 2 |
| n > 3 | (n-1)*(F(n-2) + F(n-1)) |
当 n = 3 时,上述递推关系依然成立,故整理后得到:
| n 的值 | F(n) 的值 |
|---|---|
| n = 1 | 0 |
| n = 2 | 1 | |
| n > 2 | (n-1)*(F(n-2) + F(n-1)) | |
编程实现
在一些笔试面试的时候,只要掌握了递推算法,就能很快求出具体的值。既然弄清了算法,那么对应的编程就很简单了,如下:
[[include]] <iostream>
using namespace std;
int solution(int n)
{
if(n <= 1)
{
return 0;
}
if(n == 2)
{
return 1;
}
return (n - 1) * (solution(n - 2) + solution(n - 1));
}
int main()
{
for(int n = 1; n < 10; n++)
{
cout << solution(n) << endl;
}
return 0;
}
结果:
0
1
2
9
44
265
1854
14833
133496
错位排列很有意思,也是经常涉及到的考点,关键还是在于思路。我们也会一步一个脚印,争取每篇文章讲清讲透一件事,也希望大家阅读后有所收获,心情愉快。
- EOF -